2023夏の甲子園 履正社(大阪代表)対鳥取商(鳥取代表) 予想評価は!?<高校野球/1回戦第2日>

履正社(大阪代表)対鳥取商(鳥取代表) 客観的予想評価は！？

2023年夏の甲子園2日目！
第二試合は優勝候補履正社(大阪)と鳥取商(鳥取)の対決となりました。

ブックメーカーカジ旅ではデータに基づいた客観的試合前予想オッズ評価が発表されております。

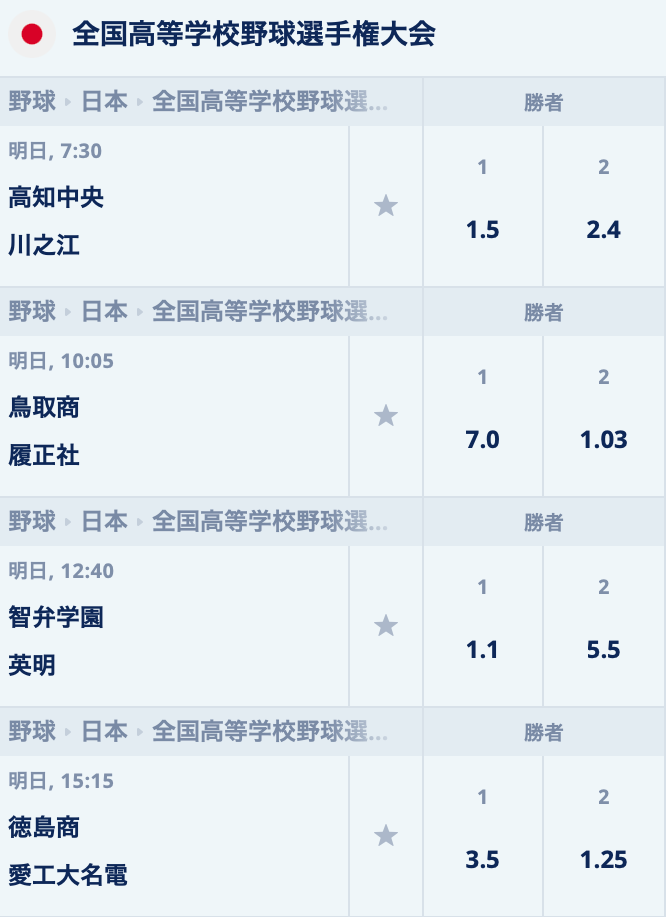
2023夏の甲子園・高校野球⚾️試合前オッズ

鳥取商の勝利 7.0倍
履正社の勝利 1.03倍

タロさ

オッズは状況によって変わっていくのでぜひ公式サイトをチェックしてみてくださいね！

※もちろん実際に賭けて遊ぶこともできますよ♪方法は下記ページにまとめました。

2023甲子園(高校野球)全試合賭けれるブックメーカー【最新】賭け方,試合予想オッズ

※ブックメーカーカジ旅とは！？

【カジ旅】スポーツブックメーカーやり方始め方！メリットデメリット徹底解説

試合前予想オッズでは大阪府代表・履正社の方が圧倒的に優勢だとの評価ですね！

履正社は4年ぶり5回目となる夏の甲子園出場。
甲子園通算成績は22勝12敗。

今や甲子園常連校の大阪桐蔭を決勝で３−０で完封するなど、強豪ぞろいの大阪府大会を勝ち抜いた猛者で、今大会優勝候補の一角とも言われております。

一方鳥取商は2年連続4回目となる夏の甲子園出場。
甲子園通算成績は0勝3敗。

鳥取大会ではチームの投手力・守備力が光り、防御率はわずか0.97を記録！
山根・荒川の2枚看板が履正社の強力打線を封じ込めるか！？

タロさ

現在カジ旅では新規プレイヤー100ドルフリーベットと50回分のフリースピン(スロット)がもらえるキャンペーン中！下記リンクより。
超絶お得なのでこのチャンスをお見逃しなく✨

カジ旅100ドルフリーベット&50回フリースピンキャンペーン中！

カジ旅100ドルフリーベット&50回フリースピンキャンペーン！

カジ旅無料登録&フリーベット獲得はこちら！

タロさ

初回フリーベット獲得方法は下記ページにまとめました！

【カジ旅ブックメーカー】初回入金フリーベットボーナスやり方獲得方法！

あわせて読みたい

【カジ旅ブックメーカー】初回入金フリーベットボーナスやり方獲得方法！ カジ旅ブックメーカーの初回入金ボーナスでフリーベットをゲットしました！ 自分のリアルマネー(入金したお金)を使わなくても賭けることができるスポーツフリーベット。...

高校野球ファンによる履正社対鳥取商 試合予想！

履正社が５−３で勝利と予想(Tさん)

履正社の投手力に注目！

激戦の大阪大会、それも決勝戦で大阪桐蔭を3対0の完封でくだし、念願の甲子園出場を果たした履正社高校の優位は動かないと思います。

そんな中でも注目したいのは、履正社高校の2人の左腕です。大阪大会の決勝戦で大阪桐蔭を完封勝利で押さえ込んだ背番号10の福田くん。秋まではエースナンバーを背負っていただけに自信を持ってこの大会に臨んだはずです。大阪大会決勝戦の様子を見る限り、実力通り力を発揮すれば、鳥取商業もなかなか打ち下す事は難しいでしょう。
仮に背番号1の増田くんが登板した際も、イニング以上の三線を奪う力は、鳥取商業にとっては間違いなくかなり驚異的なはず。

鳥取商業のエース山根くんも圧倒的な力を示すわけではありませんが、粘り強い東急で鳥取大会を接戦を勝ち抜いてきた実力は、履正社高校を苦しめることもあり得ます。鳥取商業の打線が長打力が期待できるような性格ではないこともあり、立ち上がり、履正社高校に捕まらないことが接戦に持ち込むことの最大の条件になるでしょう。履正社高校の打線が長打を狙うばかりではなく、確実性のあるヒッティングができるところも大きな魅力です。
いずれにせよ、立ち上がりにどれだけ両校の投手が安定した時を見せることができるかがポイントになるでしょう。

接戦に持ち込むことができれば、鳥取商業にも履正社の焦りを狙い、勝利の芽も見えてくるのではないでしょうか。なんといっても、お互い甲子園の初戦だけに立ち上がりのミスが禁物です。